Ed Solutions Are A Breath Away!

SHARE THIS STORY:

It’s natural to think that the answers to today’s education questions lie somewhere on a continuum between two extremes: How much autonomy should students have – all or none? Hmmmm…. probably somewhere in the middle. Where should curriculum decisions be made – in my classroom or Washington, D.C.?  Hmmmm… probably somewhere in the middle.

But finding the perfect compromise between two extremes can be fruitless and frustrating. Sometimes we need to stop and take a breath.

Let’s do it together.

Take a deep breath. Exhale. Again. Feels good, doesn’t it? Now take a deep breath and hold it. Don’t pass out! But hold it until it gets uncomfortable, then a little more, then exhale slowly. Feel the relief? Let it all out. All of it. Give it one last push. When your lungs are completely empty hold that state until it’s uncomfortable, then inhale and breathe normally.

Now, search for that perfect spot somewhere between breathing in and breathing out – The spot where you can just stop breathing forever.

Obviously, it doesn’t exist.

That’s because breathing isn’t a continuum, it’s a polarity. And readers of Polarity Management: Identifying and Managing Unsolvable Problems, by Barry Johnson, will recognize the breathing illustration.

In a polarity, Johnson writes, there is no perfect midpoint. Both end members must be attended or the system collapses. If at any point in the process you stop breathing, you collapse!

Compare that to a continuum. I like blue but I’m not fond of yellow. Yet somewhere between blue and yellow, is green – my favorite color.

The breathing example demonstrates the salient features of a polarity: There is no sustainable mid-point, and you must spend time at each extreme. That’s not true of a continuum. Who really needs to spend time with yellow?

You solve a continuum issue but you manage a polarity, according to Johnson.

Here’s a classroom example of a continuum. An eighth grade team plans an incentive field trip. The team needs to decide how many unexcused tardies make a student ineligible. One teacher says a single unexcused tardy should disqualify a student. Another says they shouldn’t count tardies at all. Everyone else falls in between. The team agrees to vote on 0, 1, 2, 3… tardies and stand by the result. Issue resolved.

Now a polarity. How much should I review in Algebra? We need to move fast, and kids who need more time can go to tutoring, so maybe we shouldn’t review at all. Or, we could spend most of every class reviewing and add just a little new content at the end.

But locking into either is too rigid.

Here’s a better approach. In algebra new content builds on old and has review built in. So a class can go several days with little or no explicit review. But kids will eventually show signs of concept fatigue. When that happens it’s time for a couple of days of pure review.

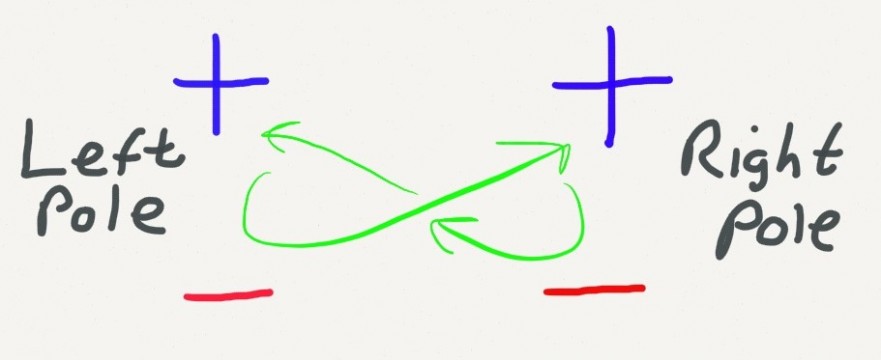
Good polarity managers, according to Johnson, can state the advantages and disadvantages of each end member. They also know what state the system is currently in, and what direction it’s moving. The aim is to keep the system in its current state as long as the advantages of that state outweigh its disadvantages. Then when the disadvantages begin to mount the task is to push the system to the other state. The drawing above, inspired by Johnson, illustrates this movement.

Pay attention to your breath for a few moments. Good polarity management is a marvel to behold.

We seem always to assume that hot button issues like teacher evaluation, Common Core, charter schools, vouchers, unions, and math instruction are continua. The result, therefore, is either winner take all or compromise. That’s fine if an issue is a continuum and the compromise is healthy or the winner correct. But if the issue is a polarity the system is doomed.  (And if the system is a continuum but the compromise is unhealthy or the winner wrong, the system is also doomed.)

I’d ask advocates in any education issue to question whether the issue might be a polarity. If so, could they not indentify conditions when each end member is more suitable? Then could they not develop protocols for deciding which end member to move toward as conditions change?

On my Digressive Discourse Blog at The Center for Teaching Quality, please read in Common Core Math Instruction: Managing a Tri-polar System how I take a stab at how we might better manage teaching math facts, comprehension, and application – a hot button issue related to the Common Core.

Sandy Merz

I grew up in Silver City, New Mexico and went the University of New Mexico, earning a Bachelor of Science degree in Geology. After working for the U.S. Geological Survey in remote regions of western New Mexico, I moved to Tucson to attend graduate school at the University of Arizona, earning a Master of Science degree in Hydrogeology. While working as an intern hydrologist for a local county agency, I started doing volunteer work that involved making presentations in schools. At that moment I knew teaching was the path to follow. It must have been a good decision because I’m still on the path after thirty-two years. My teaching certificates are in math and science and I am a National Board Certified Teacher in Career and Technical Education. After teaching engineering and math and elective classes at the same school in downtown Tucson my whole career, I've moved to a different middle school and district on the edge of town to teach math. In addition to full time teaching, I am actively involved in the teacher leadership movement by facilitating National Board candidates, blogging for Stories from School Arizona, and serving on the Arizona K12 Center’s TeacherSolutions team. In January 2017, Raytheon Missile System named me a Leader in Education and I'm a former Arizona Hope Street Fellow.